带部分粘性和阻尼的3D Boussinesq-MHD方程组的适定性
带粘性和阻尼的流体方程引起了广大数学研究者的兴趣。如:带阻尼项的3维micropolar方程组强解的存在性、带部分粘性和阻尼的3D Boussinesq-MHD(Magnetohydrodynamics,简称MHD)方程组的适定性等。
文理学院林琳与曲阜师范大学数学科学学院刘辉、南京财经大学应用数学学院孙成峰合作,运用能量方法,研究了带部分粘性和阻尼的3维Boussinesq-MHD方程组整体解的存在唯一性。磁流体力学MHD是研究等离子体和磁场相互作用的物理学分支。MHD-Boussinesq系统模拟由热场或密度场的浮力效应和磁场产生的洛伦兹力驱动的不可压缩流体的对流,这种对流发生在存在磁场的导电流体的水平层,它与Rayleigh-Benard对流的自然类型密切相关,在应用中有着很强的实际意义。
该研究成果近期已发表期刊《Journal of Mathematical Analysis and Applications》。
高质量Cu2O/ZnO异质结薄膜太阳电池及界面调控机理研究
宽禁带氧化物薄膜异质结广泛应用在半导体光电子器件领域,也有望应用于晶硅太阳电池的顶电池、钝化层等光伏领域,提高晶硅太阳电池的光利用率、降低背表面载流子复合,提高开路电压和短路电流,提高光电转换效率,降低发电成本。
材料学院王相虎团队在上海市自然科学基金、国家自然科学基金等项目的资助下,成功研制出Cu2O/ZnO异质结薄膜太阳电池,该太阳电池制备温度低、热稳定性高,标准测试条件下,光电转换效率达到3.9%。同时,研究发现,富氧条件下获得的ZnOX(X>1)薄膜,能够很好对PERC电池的背面进行有效钝化,提高了转换效率。相关结果发表在《Materials Today Physics》、《Journal of Alloys and Compounds》和《 Nanomaterials》等期刊上,申请国家发明专利1项。
面向海上风机变桨系统的故障诊断与智能维护
在“十四五”期间,国家将积极支持海上风电集中连片规模化开发,开展故障诊断与智能维护是实现海上风机安全运行的重要保障,而对其关键部件变桨系统及相关部件的诊断方法研究显得尤为重要。
电气学院文传博团队与上海电气风电集团项目团队合作,针对变桨限位开关和叶片角度不一致等故障,基于变桨系统的二阶模型与监测数据相结合的方法开展故障诊断研究。研究结果表明该方法对实现上述两类故障的诊断具有效果良好。针对叶片损伤的检测问题,课题组提出了一种基于YOLOv5 的UAVs图像分析的WTB表面缺陷检测的高精度模型SOD-YOLO。该项研究成果在原始的YOLOv5中引入微尺度检测层,采用K-means算法重新聚类anchors并添加CBAM注意力机制到每个特征融合层,减少小目标缺陷和其他缺陷的特征信息丢失。此外,为提高检测效率,采用通道剪枝算法减小模型尺寸,能够快速、有效地检测小目标缺陷和其他缺陷。
该研究成果近期发表于《Advanced Theory and Simulations》、《Neurocomputing》和《Journal of Renewable and Sustainable Energy》。
电气学院在神经网络和人工智能领域取得新进展
近日,我校电气学院陈利娟老师作为第一作者和通讯作者,我校作为第一单位和通讯单位,与上海理工大学、电子科技大学、四川大学、德国汉堡大学德国国家工程院院士团队合作,在国际知名期刊NEUROCOMPUTING和NEURAL NETWORKS上分别发表题为“State estimation for memristive neural networks with mixed time varying delays via multiple integral equality”和“Semantic consistency learning on manifold for source data-free unsupervised domain adaptation”的学术研究论文。NEUROCOMPUTING(IF=5.779)和NEURAL NETWORKS(IF=9.657)在神经网络和人工智能领域具有很高的学术声誉。
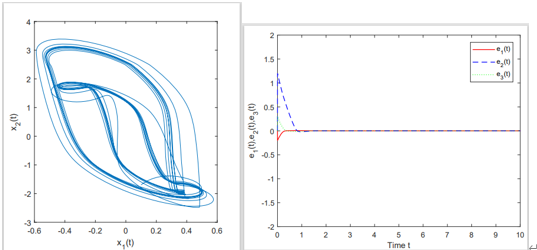
基于忆阻器的神经网络具有低功耗、高度可扩展、高度可适应等特点,对于突破当前基于“冯·诺依曼”架构的神经网络计算瓶颈具有重要意义。作为忆阻神经网络中的典型特征,时滞是造成系统不稳定的关键因素之一。针对该问题,陈利娟老师提出了混合时滞的忆阻神经网络状态估计问题,研究混合时滞忆阻神经网络保守性,通过非脆弱状态估计,建立基于估计误差的系统渐近稳定充分条件,提供了保守性判定的理论依据,为忆阻交叉阵列等真实忆阻神经网络的设计提供了理论指导。

此外,针对无源无监督领域自适应这一热点迁移学习问题,陈利娟老师等提出了一种基于流形语义一致性的深度学习方法。该方法通过挖掘隐藏在数据流形中的具有语义关联的几何约束关系,有效克服了目标领域语义标签缺失,实现了基于自监督学习的模型迁移,在开源的标准数据上,取得了SOTA的性能。由于并不需要源领域的任何数据,该方法在涉及隐私保护、信息安全的人工智能应用中具有独特优势。
以上两项工作陈利娟老师均依托上海电机学院博士科研启动基金完成。